GEOMETRÍA 8°

                                            COLEGIO CAMPESTRE GARDNER
    INTELIGENCIAS MÚLTIPLES APLICADAS

MATERIA:GEOMETRÍA   

DOCENTE:Leidi Johana Jimenez

FECHA: 01 -OCTUBRE-2020

HORA DE INICIO:8:00am   

HORA DE ENTREGA:3:00pm

CORREO DE ENVÍO: leidizenemij@hotmail.es

Líneas notables en el triángulo

En un triángulo se pueden trazar rectas o segmentos notables que gozan de propiedades importantes. En este artículo consideramos a las bisectrices y a las mediatrices.

Bisectriz

Como se estudió en lecciones anteriores, la bisectriz de un ángulo es el rayo que lo divide en dos ángulos de igual medida. Observa el ángulo $AOB$A, O, B que se ha dividido en $2$2 ángulos iguales, cada uno de los cuales mide $\alpha$alpha grados.

Considera que este ángulo, también se puede representar mediante símbolos. Así tenemos: $\angle AOB$angle, A, O, B cuya medida es $2\alpha$2, alpha grados.

Angulo abertura

En esta lección estudiaremos las bisectrices de los ángulos interiores y exteriores de un triángulo.

Bisectriz interior

Es el rayo que divide a un ángulo interior del triángulo en dos ángulos congruentes.

Bisectriz interior

En el gráfico, se observa que $\overline{AD}$start overline, A, D, end overline es una bisectriz interior del triángulo $ABC$A, B, C respecto al ángulo $A$A y relativa al lado $\overline{BC}$start overline, B, C, end overline. Esto quiere decir que va del vértice $A$A e intercepta a $\overline{BC}$start overline, B, C, end overline.

Como la bisectriz parte de un vértice, en un triángulo podemos trazar $3$3 bisectrices interiores cuya intersección es el punto $I$I denominado incentro.

En la siguiente animación se manipulan los puntos $A$A, $B$B y $C$C para visualizar la ubicación del incentro y las características de las bisectrices interiores de un triángulo:

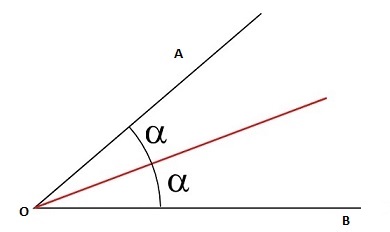
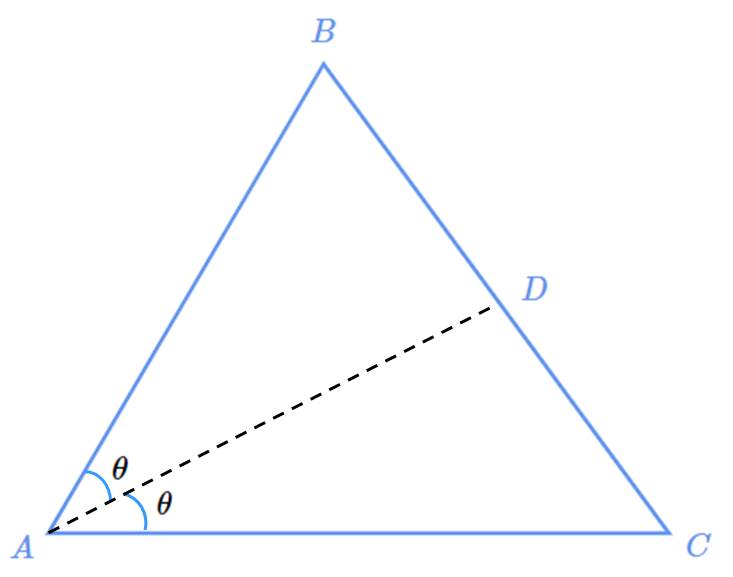
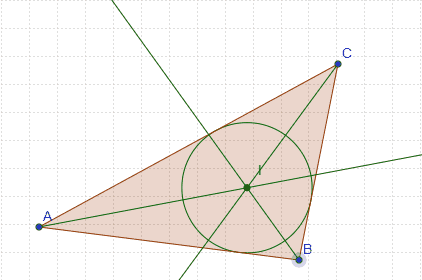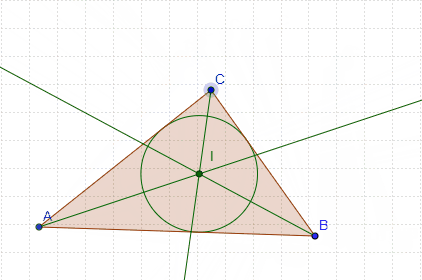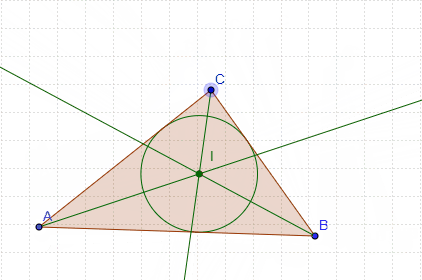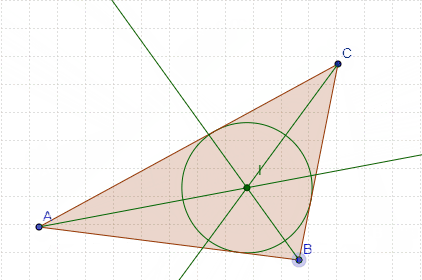
Bisectriz interior

Bisectriz exterior

En un triángulo, la bisectriz exterior es el rayo que divide a un ángulo exterior del triángulo en dos ángulos congruentes.

CLASE DEL 01 DE OCTUBRE

CARACTERÍSTICAS  DE LAS LINEAS NOTABLES DEL TRIÁNGULO.

CLASE DEL 15 DE OCTUBRE

ACTIVIDAD

1) REALIZA  LA PÁGINA  166 DEL LIBRO DE MATEMÁTICAS DEL PUNTO 13 AL 24

 

CLASE DEL 29 DE OCTUBRE

MOVIMIENTOS EN EL PLANO 

Traslación: es el movimiento directo de una figura en la que todos sus puntos:

• Se mueven en la misma dirección.
• Se mueven la misma distancia.

El resultado de una traslación es otra figura idéntica que se ha desplazado una distancia en una dirección determinada.

Cuando movemos un mueble en una misma dirección lo estamos trasladando. El tren se traslada a lo largo de una vía recta. El ascensor nos traslada de una planta a otra... Estas y muchas otras más son situaciones en las que el movimiento de traslación está presente en nuestras vidas.

Rotación o giro: es un movimiento alrededor de un punto que mantiene la forma y el tamaño de la 

figura original.

Una rotación se determina por estos tres elementos:

• Un ángulo que determina la amplitud de la rotación.
• Un punto llamado centro de rotación.
• Un sentido de la rotación que puede ser del mismo sentido de las agujas del reloj o en sentido contrario.

La vida cotidiana está llena de situaciones en las que la rotación o giro está presente. Cuando abrimos o cerramos una puerta estamos haciendo una rotación sobre un punto o centro de rotación, las ruedas de nuestra bicicleta giran sobre el eje central, al igual que los pedales, giramos al montar en los caballitos, al abrir y cerrar el abanico hacemos que gire sobre un punto, al mover la ruleta hacemos que gire igualmente sobre su centro. 

Simetría: 

La simetría respecto a un eje es una reflexión. 

Los cuerpos se reflejan en el agua, en una superficie pulida, en los espejos. El objeto que vemos reflejado decimos que es su simétrico.

Este tipo de simetría, con respecto a un eje, se caracteriza porque:

• Los puntos simétricos de una figura y los de la figura reflejada están sobre la misma línea.
• Los puntos de ambas figuras están a la misma distancia del eje de simetría en direcciones opuestas.
• La figura reflejada siempre tiene el mismo tamaño, pero en la dirección opuesta.

En nuestra vida cotidiana, al igual que en la naturaleza, nos encontramos con multitud de situaciones en las que está presente la simetría... si nos fijamos en nuestro cara veremos que ojos, nariz, orejas, boca son simétricas respecto a un eje imaginario. 

 CLASE DEL 05 DE NOVIEMBRE