clase del 15 de septiembre
inicio del cuarto periodo
FUNCIÓN EXPONENCIAL
En el ámbito de las matemáticas, una función es un vínculo entre dos conjuntos mediante el cual a cada elemento del primer conjunto le es asignado un único elemento del segundo conjunto o ninguno. Exponencial, por otra parte, es un adjetivo que califica al tipo de crecimiento cuyo ritmo se incrementa cada vez más rápido.
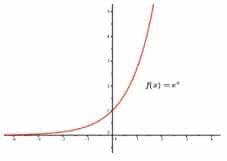
De acuerdo a sus características, existen diversos tipos de funciones matemáticas. Una función exponencial es una función que se representa con la ecuación f(x) = aˣ, en la cual la variable independiente (x) es un exponente.
Una función exponencial, por lo tanto, permite aludir a fenómenos que crecen cada vez con mayor rapidez.
CLASE DEL 22 DE SEPTIEMBRE
La forma general de la función exponencial es del tipo:

Sea a un número real. La función que a cada número real x le hace corresponder
la potencia ax se llama función exponencial de base a y exponente .
Ejemplos


| x | y = 2x |
|---|---|
| -3 | 1/8 |
| -2 | 1/4 |
| -1 | 1/2 |
| 0 | 1 |
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |


| x | y = (½)x |
|---|---|
| -3 | 8 |
| -2 | 4 |
| -1 | 2 |
| 0 | 1 |
| 1 | 1/2 |
| 2 | 1/4 |
| 3 | 1/8 |
- CLASE DEL 24 DE SEPTIEMBRE
- ACTIVIDAD
- 1) Representa gráficamente y di las propiedades de la función g cuya ecuación es g(x) = 3x+2 Y 5x – 25 analiza la gráficas. utiliza el graficador de Geo-gebra
Propiedades de la función logarítmica
Todas las funciones logarítmicas cumplen las siguientes propiedades:
- Función logarítmica del producto:

- Función logarítmica de la división:

- Función logarítmica del inverso multiplicativo:

- Función logarítmica de la potencia:

Logaritmos
Sean dos números reales a y b, siendo a ≠ 1. El logaritmo en base a de b es el elemento al que hay que elevar el número a para dé como resultado el número b.
Por ejemplo, el logaritmo en base 3 de 9 es 2, ya que siendo a = 3 y b = 9, el número al que hay que elevar 3 para que dé 9 es 2, 32 = 9.
Cuando el logaritmo es en base 10 (a = 10), se llama logaritmo decimal y no se suele escribir la base: f(x) = log x. También se llaman algoritmos comunes.
Normalmente, cuando no se especifica la base, se entiende como función logarítmica la que tiene de base el número e (a = e = 2,7182818…). En este caso se llama logaritmo neperiano (o logaritmo natural) y suele escribirse: f(x) = ln x.
El logaritmo de un producto es igual a la suma de los logaritmos de los factores


2 El logaritmo de un cociente es igual a la diferencia del logaritmo del dividendo y el logaritmo del divisor


3 El logaritmo de una potencia es igual al producto del exponente por el logaritmo de la base


4El logaritmo de una raíz es igual al cociente entre el logaritmo del radicando y el índice de la raíz
![Rendered by QuickLaTeX.com \displaystyle \log\sqrt[n]{A} = \frac{\log A}{n} = \frac{1}{n}\cdot \log A](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-c85421036315669e7d770159a75e09ab_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \log_{2}(\sqrt[4]{8})=\frac{1}{4}\cdot \log_{2}(8)=\frac{1}{4}\cdot 3=\frac{3}{4}](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-76bf9700f517ec604b0186ca9a417733_l3.png)
De las propiedades  y
y  podemos deducir que:
podemos deducir que:
![Rendered by QuickLaTeX.com \displaystyle \log\sqrt[n]{A^{m}} = \frac{m\cdot \log A}{n} = \frac{m}{n}\cdot \log A](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-9c4da73542f0bd0c73266e1d2d43edde_l3.png)
5 El logaritmo base ' ' de '
' de ' ' es
' es  .
.

6 El logaritmo de  es
es  (Sin importar la base del logaritmo)
(Sin importar la base del logaritmo)

Por lo tanto:


7 El argumento de un logaritmo siempre debe ser mayor que cero
Para  se cumple que
se cumple que 
Función logarítmica
La función logarítmica en base  es la función inversa de la exponencial en base
es la función inversa de la exponencial en base  .
.



















No hay comentarios.:
Publicar un comentario