El mundo de las Matemáticas: TRIGONOMETRIA 10°

TRIGONOMETRIA 10°

COLEGIO CAMPESTRE GARDNER

INTELIGENCIAS MÚLTIPLES APLICADAS

MATERIA:TRIGONOMETRIA

DOCENTE:Leidi Johana Jimenez

FECHA:01-OCTUBRE 2020

HORA DE INICIO:8:00am

HORA DE ENTREGA:3:00pm

CORREO DE ENVÍO: leidizenemij@hotmail.es

CLASE DEL 15 DE SEPTIEMBRE
INICIO DEL CUARTO PERIODO

Las cónicas

Se denomina sección cónica (o simplemente cónica) a todas las curvas intersección entre un cono y un plano; si dicho plano no pasa por el vértice, se obtienen las cónicas propiamente dichas. Se clasifican en tres tipos: elipse, parábola e hipérbola. un cono circular recto de dos hojas con un plano que no pasa por su vértice
De acuerdo al ángulo y el lugar de la intersección es posible obtener circulos, hiperbolas , elipses o parabolas. Cuando el plano solo toca uno de los mantos del cono y no es paralelo a una de sus aristas se obtiene una Elipse. Cuando el plano corta los dos mantos del cono se obtiene una hiperbola. Cuando el plano que corta es paralelo a una de las aristas del cono se obtiene una parábola.

Elementos de las cónicas

Superficie - una superficie cónica de revolución está engendrada por la rotación de una recta alrededor de otra recta fija, llamada eje, a la que corta de modo oblicuo.
Generatriz - la generatriz es una cualquiera de las rectas oblicuas.
Vértice - el vértice es el punto central donde se cortan las generatrices.
Hojas - las hojas son las dos partes en las que el vértice divide a la superficie cónica de revolución.
Sección - se denomina sección cónica a la curva intersección de un cono con un plano que no pasa por su vértice. En función de la relación existente entre el ángulo de conicidad $(\alpha )$ y la inclinación del plano respecto del eje del cono $(\beta )$ , pueden obtenerse diferentes secciones cónicas.

CLASE DEL 22 DE SEPTIEMBRE

Tipos y aplicaciones de las Cónicas

En función de la relación existente entre el ángulo de conicidad (α) y la inclinación del plano respecto del eje del cono (β), pueden obtenerse diferentes secciones cónicas, a saber:
β > α : Hipérbola (naranja)
β = α : Parábola (azulado)
β < α : Elipse (verde)
β = 90º: Circunferencia (un caso particular de elipse rojo)

Clase del 29 de septiembre

CLASE DEL 29 DE SEPTIEMBRE

LA PARÁBOLA

La parábola es el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado foco y de una recta fija llamada directriz.

Elementos de la parábola:

1Foco: Es el punto fijo F.
2Directriz: Es la recta fija d.
3Parámetro: Es la distancia del foco a la directriz, se designa por la letra p.
4Eje: Es la recta perpendicular a la directriz que pasa por el foco.
5Vértice: Es el punto de intersección de la parábola con su eje.
6Radio vector: Es un segmento que une un punto cualquiera de la parábola con el foco.
ACTIVIDAD
1) En base a la ecuación de las siguientes parábolas determina las coordenadas de sus focos, ecuaciones de sus directrices, distancia de sus lados rectos y la gráfica.
$6y^2-12x=0$
SOLUCIÓN

clase del 13 de octubre
$2y^2=-7x$

$15x^2=-42y$

CLASE DEL 15 DE OCTUBRE

CLASE DEL 20 DE OCTUBRE

ELEMENTOS DE LA ELIPSE

Los siguientes elementos se encuentran en cada elipse:
Centro: Es el punto de intersección de los ejes. Es, además, centro de simetría.
Eje principal o focal: Es el eje en el que se encuentran los focos. Es un eje de simetría.
Eje secundario: Es el eje perpendicular al eje principal, mediatríz del segmento que une los focos.
Vértices: Puntos de intersección de la elipse con los ejes.
Distancia focal: Distancia entre los focos. Su longitud es 2·c.
Semidistancia focal: Distancia entre el centro y cada foco. Su longitud es c.
Semieje mayor o principal: Segmento entre el centro y los vértices del eje principal. Su longitud es a.
Semieje menor o secundario: Segmento entre el centro y los vértices del eje secundario. Su longitud es b y cumple $b = \sqrt{a^{2} - c^{2}}$
Radio vectores: Cada punto de la elipse cuenta con dos radio vectores que son los segmentos que unen dicho punto a cada uno de los focos. Para un punto P(x , y) se cumple que d(P , F) = a -e·x y d(P, F') = a+e·

CLASE DEL 22 DE OCTUBRE

Hallar la ecuación de lugar geométrico de los puntos $P(x,y)$ $P(x, y)$ cuya suma de distancias a los puntos fijos
$F_1(4,2)$ y $F_2(-2,2)$ sea igual a $8$ .

Buscamos que la suma de las distancias $\overline{PF_1}$ y $\overline{PF_2}$ sea siempre igual a $8$ , es decir,
$\displaystyle \overline{PF_1} + \overline{PF_2} = 8$ Por lo tanto, tenemos que,
$\displaystyle \sqrt{(x + 2)^2 + (y - 2)^2} + \sqrt{(x - 4)^2 + (y - 2)^2} = 8$
Si despejamos una raíz, se obtiene
$\displaystyle \sqrt{(x + 2)^2 + (y - 2)^2} = 8 - \sqrt{(x - 4)^2 + (y - 2)^2}$
Luego, elevando al cuadrado, tenemos que
$\displaystyle (x+2)^2 + (y-2)^2 = 64 - 16\sqrt{(x - 4)^2 + (y - 2)^2} + (x -4)^2 + (y - 2)^2$
Observemos que el término $(y-2)^{2}$ se encuentra a ambos lados de la ecuación. Por tanto, podemos cancelarlo, de manera que nos queda
$\displaystyle (x+2)^2 = 64 - 16\sqrt{(x - 4)^2 + (y - 2)^2} + (x -4)^2$
Si expandimos los dos binomios al cuadrado, tendremos que,
$\displaystyle x^2 + 4x + 4 = 64 - 16\sqrt{(x - 4)^2 + (y - 2)^2} + x^2 - 8x + 16$
Luego, reagrupando términos semejantes $)-y$ dividiendo la ecuación por $4$ —, tenemos
$\displaystyle 3x - 19 = -4 \sqrt{(x - 4)^2 + (y - 2)^2}$
Ya nos deshicimos de un radical. Para deshacernos del otro repetimos el procedimiento. Elevamos al cuadrado la expresión, expandemos los binomios al cuadrado y reagrupamos términos:
$\displaystyle 9x^2 - 114x + 361 = 16\left((x - 4)^2 + (y - 2)^2 \right)$
es decir,
$\displaystyle 7x^2 + 16y^2 - 14x - 64y - 41 = 0$

CLASE DEL 27 DE OCTUBRE

Definición de hipérbola

Una hiperbola se define como el lugar geométrico de los puntos del plano en el que la diferencia de distancias a dos puntos fijos denominados focos, F y F', es siempre constante.
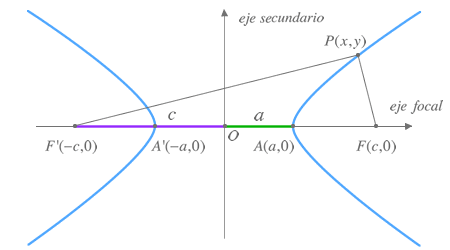
Hipérbola
Las líneas azules constituyen lo que se conoce como una hipérbola. Observa sus focos F y F'. Estos puntos son muy importantes ya que la diferencia de la distancia entre cada punto P(x,y) y estos puntos es siempre constante.
Por tanto, debes tener en cuenta que para cualquier punto de la hipérbola siempre se cumple que:
dP,F-d(P,F')=2·a
Donde d(P,F) y d(P,F') es la distancia de un punto genérico P de la hipérbola al foco F y al foco F' respectivamente. Y donde 2a es una constante

Elementos de la hipérbola

En las hipérbolas podemos distinguir ciertos elementos comunes que se detallan a continuación
Focos (F y F'). Puntos fijos en los que la diferencia de distancia entre ellos y cualquier punto de la hipérbola es siempre la misma
Eje focal, principal o real. Recta que pasa por los focos.
Eje secundario o imaginario. Mediatriz del segmento que une los dos focos.
Centro (O). Punto de intersección de los ejes focal y secundario.
Semidistancia focal (c). La mitad de la distancia entre los dos focos F y F'. Su valor es

CLASE DEL 29 DE OCTUBRE

EJEMPLO:

$\frac{x^2}{144} - \frac{y^2}{81} = 1$
De la ecuación de la hipérbola se obtiene
${\begin{array}{lcl}a^2 = 144 & \Longrightarrow & a=12 \\\\ b^2 = 81 & \Longrightarrow & b=9 \end{array}}$
Encontramos el valor de ${c}$
${c = \sqrt{a^2 + b^2} \ \ \ \Longrightarrow \ \ \ c = \sqrt{144 + 81} = 15}$
Conociendo ${a, b, c}$ , que la hipérbola se encuentra centrada en el origen y su eje real es horizontal, ya podemos encontrar los vértices ${A_1, A_2}$ , los focos, ${F_1, F_2}$ y la excentricidad ${e}$
${A_1 = (-a, 0), \ A_2=(a, 0) \ \ \ \Longrightarrow \ \ \ A_1 = (-12, 0), \ A_2 = (12, 0)}$
${F_1 = (-c, 0), \ F_2=(c, 0) \ \ \ \Longrightarrow \ \ \ F_1 = (-15, 0), \ F_2 = (15, 0)}$
${e = \displaystyle \frac{c}{a} \ \ \ \Longrightarrow \ \ \ e = \displaystyle \frac{15}{12} = \frac{5}{4}}$
Con los datos anteriores, representamos gráficamente la hipérbola

CLASE DEL 05 DE NOVIEMBRE

No hay comentarios.:

Publicar un comentario

Suscribirse a: Entradas (Atom)