CORREO DE ENVÍO: leidizenemij@hotmail.es
Fracciones y decimales
Las cantidades se puede expresar con fracciones y decimales. En este apartado vamos a aprender como pasar de fracción a decimal y de decimal a fracción.
Convertir fracción en decimal
Para convertir fracciones a decimales hacemos la división entre el numerador y el denominador.
Por ejemplo:
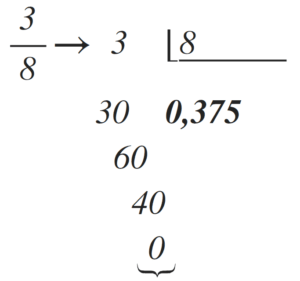
De modo que el resultado es:
Para convertir un decimal a fracción colocamos en el numerador todas las cifras sin decimales y en el denominador colocamos el 1 seguido de tantos 0 como cifras decimales tenga el número.Convertir decimal en fracción
Por ejemplo:
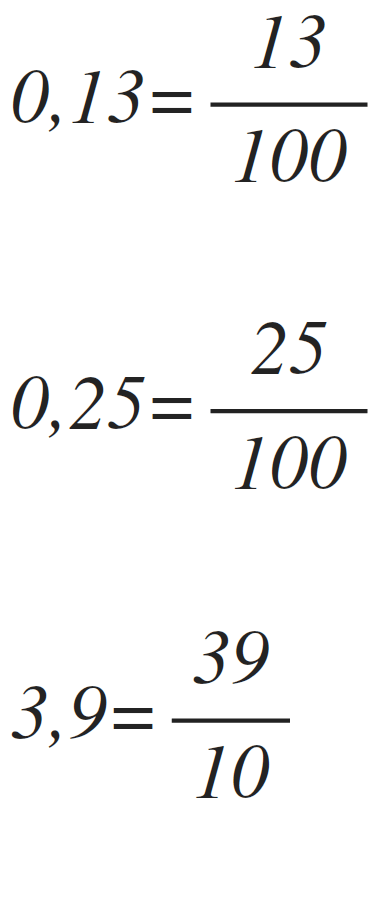
Para sumar o restar números decimales:
1 Se colocan en columnas haciendo corresponder las comas.
2 Se suman (o se restan) unidades con unidades, décimas con décimas, centésimas con centésimas...


2

Para multiplicar números decimales, se multiplican como si fueran números naturales y, en el producto, se separan con una coma, hacia la izquierda, tantas cifras decimales como tengan en total los dos factores.
Prioridad de operaciones
Las reglas de jerarquía y orden de operaciones también valen para los números decimales.
Recuerda:
- Paréntesis.
- Potencias.
- Productos y divisiones.
- Sumas y restas.
Por ejemplo:
13,8 + 12,3 x (5,1 + 2) = 13,8 + 12,3 x 7,1 = 13,8 + 87,33 = 101,13
Para multiplicar un número decimal por la unidad seguida de ceros, se desplaza la coma a la derecha tantos lugares como ceros siguen a la unidad. Si es necesario, se añaden ceros a la derecha.
- 23,87 x 10 = 238,7
- 284,2 x 100 = 28.420
- 0,4 x 1000 = 400
Razón y proporción
¿Qué es la razón entre dos números?
La razón entre dos números es el resultado de dividir dicho números.
Por ejemplo, la razón entre 4 y 2 es 2, ya que es el resultado realizar el cociente de esos dichos números.

La razón no se mide en ninguna unidad.
Al dividir dos números entre sí, lo que estamos haciendo es comparar el primer número con el segundo número, por tanto, la razón nos sirve para indicar cuántas veces el primer número es el segundo número, o lo que es lo mismo, por qué número hay que multiplicar el segundo número para obtener el primero.
En el ejemplo anterior, cuando calculamos la razón entre 4 y 2, estamos comparando 4 con 2 y que la razón sea 2 nos indica que 4 es 2 veces 2, es decir, es el doble.
la razón entre dos números comparamos el primer número entre el segundo número. Así que, ten en cuenta el primer número no tiene por que ser siempre el mayor de los dos.
También podemos calcular la razón entre 2 y 4, que es 0,5:

Sólo tienes que tener en cuenta que a la hora de definir la razón entre esos dos números, tienes que nombrar primero al número que colocas en el numerador, ya que comparas el número que está en el numerador con el que está en el denominador.
En una frutería hay 25 manzanas y 35 naranjas. ¿Cuál es la razón entre manzanas y naranjas? ¿Y entre naranjas y manzanas? ¿Qué nos indica cada razón?
La razón entre manzanas y naranjas es:

Lo que indica que el número de manzanas es 0,71 veces el número de naranjas.
Por otro lado, la razón entre naranjas y manzanas es:

Lo que indica que el número de naranjas es 1,4 veces que el número de manzanas
Decir que el número de manzanas es 0,71 veces el número de naranjas y que el número de naranjas es 1,4 veces que el número de manzanas es lo mismo.








profe esque no entendi el primer punto
ResponderBorrar1) Del libro de matemáticas conlógica 6 vamos a resolver los puntos del 1 al 7 de la página 17 esque no hay ningún punto que se ñame así de esa pagina
ResponderBorrar1) Del libro de matemáticas conlógica 6 vamos a resolver los puntos del 1 al 7 de la página 17 profe no hay ningun punto que se llama asi
ResponderBorrar